|
| |
Physics 3309 Homework 9
Chapter 8
8-7. Since 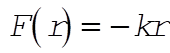 is a central force, angular momentum is conserved and the areal velocity, is a central force, angular momentum is conserved and the areal velocity, 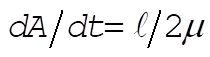 , is trivially constant (see Section 8.3). In order to compute , is trivially constant (see Section 8.3). In order to compute 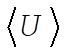 , we start with , we start with
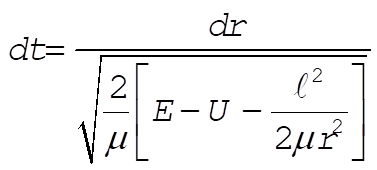 (1) (1)
and
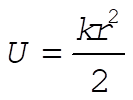 (2) (2)
The time average of the potential energy becomes
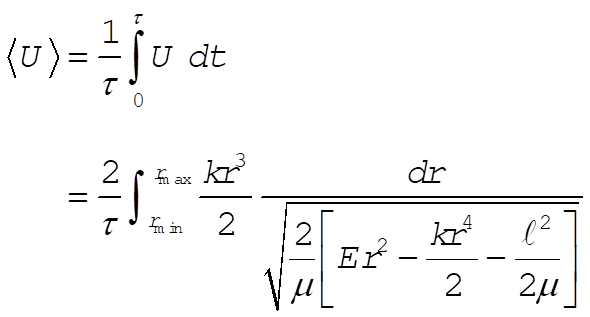 (3) (3)
Substituting
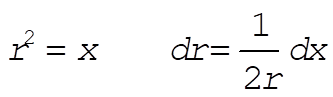 (4) (4)
(4) becomes
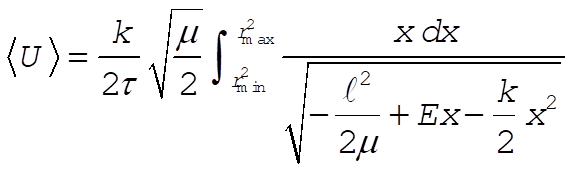 (5) (5)
Using the integrals in Eqs. (E.9) and (E.8c), Appendix E,
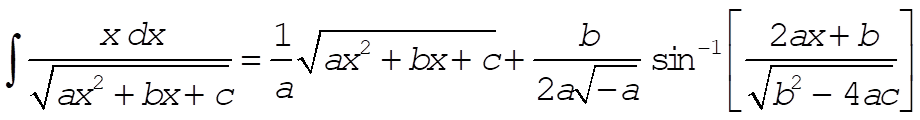 (6) (6)
(5) becomes
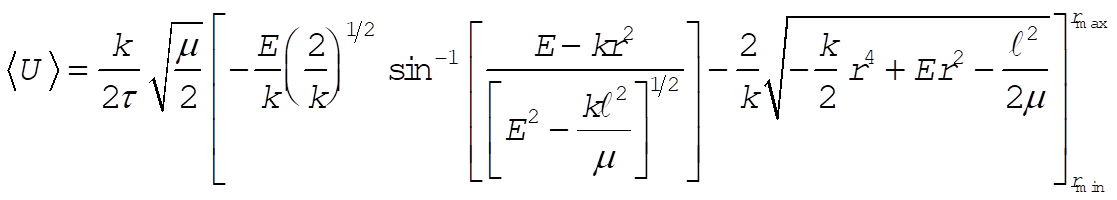 (7) (7)
But 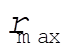 and and 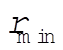 were originally defined as the roots of were originally defined as the roots of 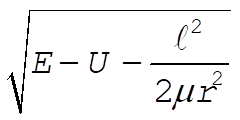 . Hence, the second term vanishes at both limits of integration. On the other hand, . Hence, the second term vanishes at both limits of integration. On the other hand,
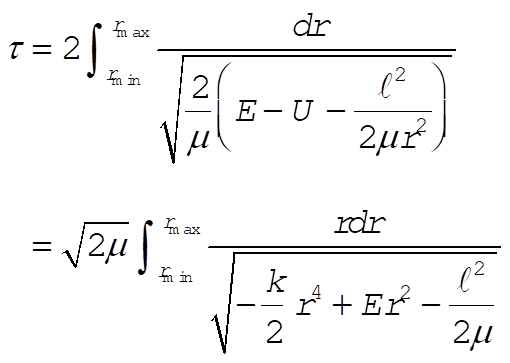 (8) (8)
or, using (5),
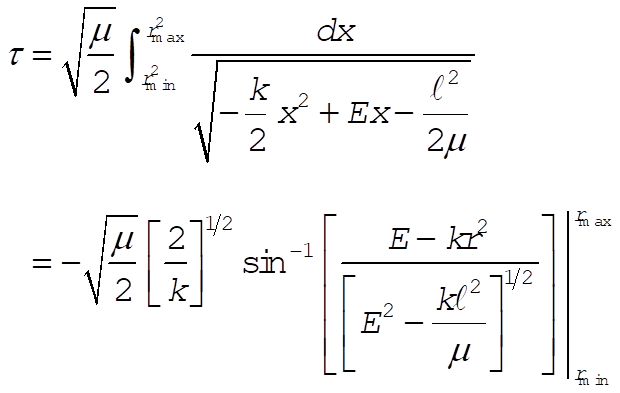 (9) (9)
Using (9) to substitute for t in (7), we have
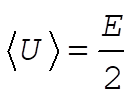 (10) (10)
Now,
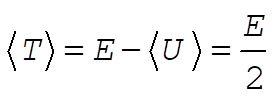 (11) (11)
The virial theorem states:
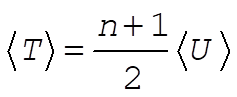 when when 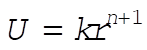 (12) (12)
In our case n = 1, therefore,
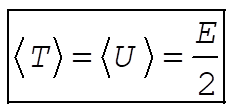
8-11. For central-force motion the equation of orbit is [Eq. (8.21)]
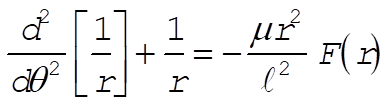 (1) (1)
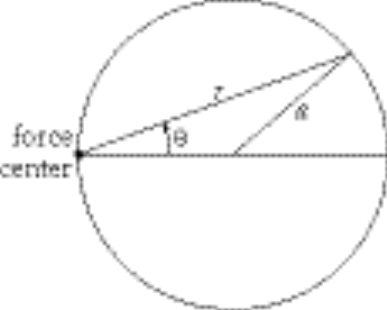
In our case the equation of orbit is
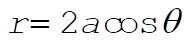 (2) (2)
Therefore, (1) becomes
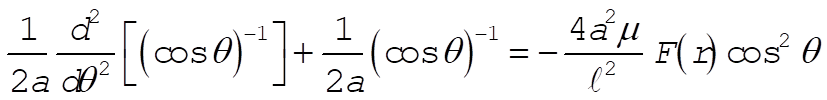 (3) (3)
But we have
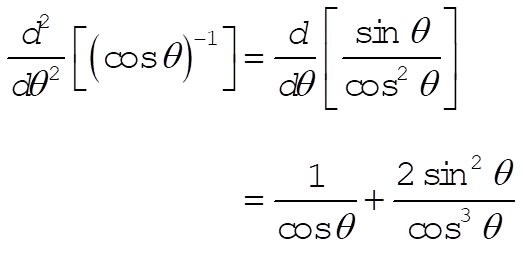 (4) (4)
Therefore, we have
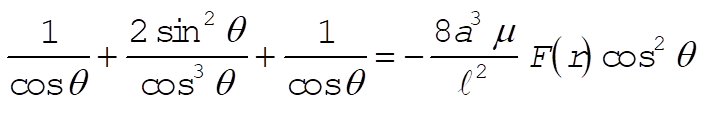 (5) (5)
or,
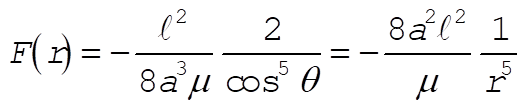 (6) (6)
so that
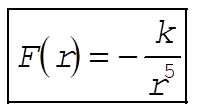 (7) (7)
8-14. The orbit equation for the central-force field is [see Eq. (8.17)]
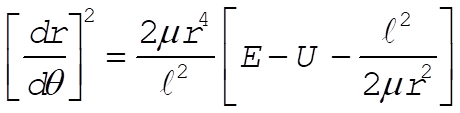 (1) (1)
But we are given the orbit equation:
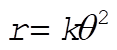 (2) (2)
from which
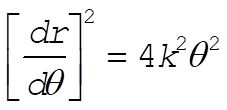 (3) (3)
Substituting (2) into (3), we have
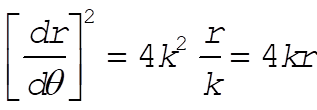 (4) (4)
From (1) and (4), we find the equation for the potential U:
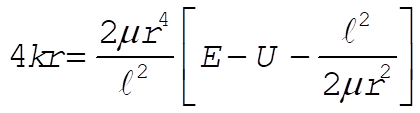 (5) (5)
from which
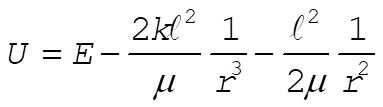 (6) (6)
and 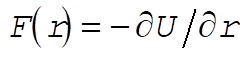 . Therefore, . Therefore,
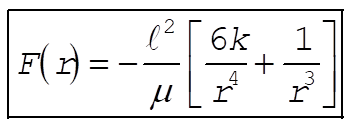 (7) (7)
8-17. The equation of the orbit is
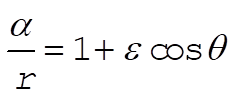 (1) (1)
from which
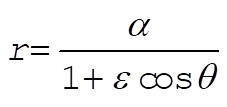 (2) (2)
where 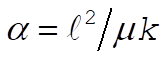 and and 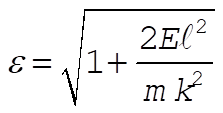 . Therefore, the radial distance r can vary from the maximum value . Therefore, the radial distance r can vary from the maximum value 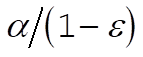 to the minimum value to the minimum value 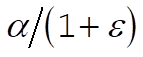 . Now, the angular velocity of the particle is given by . Now, the angular velocity of the particle is given by
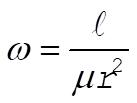 (3) (3)
Thus, the maximum and minimum values of w become
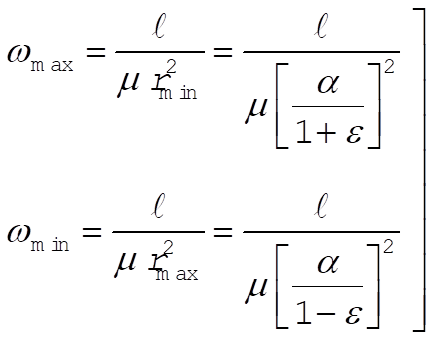 (4) (4)
Thus,
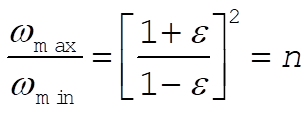 (5) (5)
from which we find
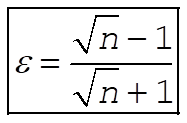 (6) (6)
8-23. Start with the equation of the orbit:
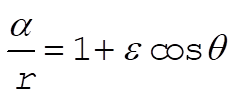 (1) (1)
and take its time derivative
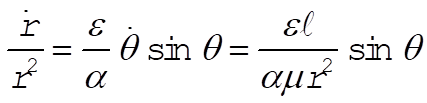 (2) (2)
Now from Equation (8.45) and (8.43) we have
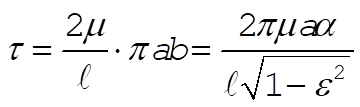 (3) (3)
so that from (2)
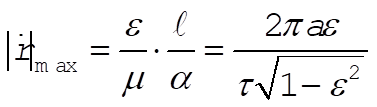 (4) (4)
as desired.
8-27. By conservation of angular momentum
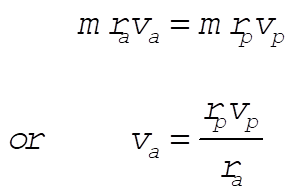
Substituting gives
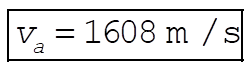
8-31. From the given force, we find
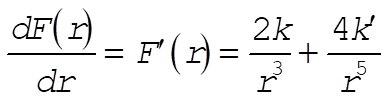 (1) (1)
Therefore, the condition of stability becomes [see Eq. (8.93)]
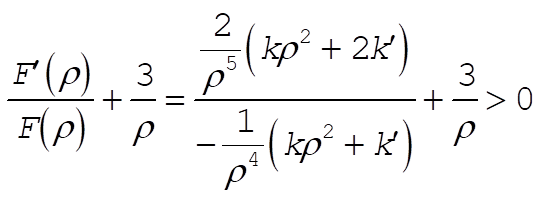 (2) (2)
or,
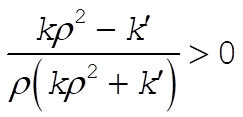 (3) (3)
Therefore, if 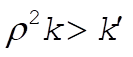 , the orbit is stable. , the orbit is stable.
8-35. If we write the radial distance r as
 (1) (1)
then x obeys the oscillatory equation [see Eqs. (8.88) and (8.89)]
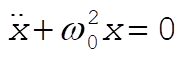 (2) (2)
where
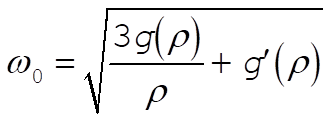 (3) (3)
The time required for the radius vector to go from any maximum value to the succeeding minimum value is
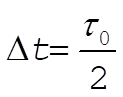 (4) (4)
where 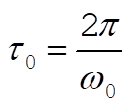 , the period of x. Thus, , the period of x. Thus,
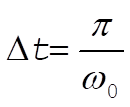 (5) (5)
The angle through which the particle moves during this time interval is
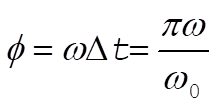 (6) (6)
where w is the angular velocity of the orbital motion which we approximate by a circular motion. Now, under the force 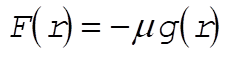 , w satisfies the equation , w satisfies the equation
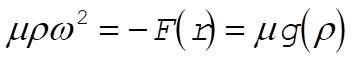 (7) (7)
Substituting (3) and (7) into (6), we find for the apsidal angle
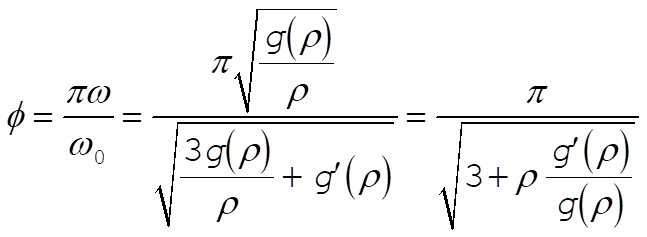 (8) (8)
Using 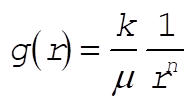 , we have , we have
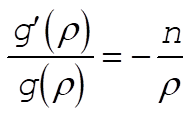 (9) (9)
Therefore, (8) becomes
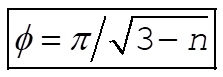 (10) (10)
In order to have the closed orbits, the apsidal angle must be a rational fraction of 2p. Thus, n must be
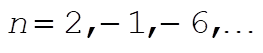
n = 2 corresponds to the inverse-square-force and n = –1 corresponds to the harmonic oscillator force.
At this point, you can go to the 3309 page,
the UH Space Physics Group
Web Site, or my personal Home Page.
Edgar A. Bering, III ,
Edgar A. Bering, III , <eabering@uh.edu>
|
 Homework 9
Homework 9