|
| |
Physics 3309 Homework 2
Chapter 1
1-31.
a)
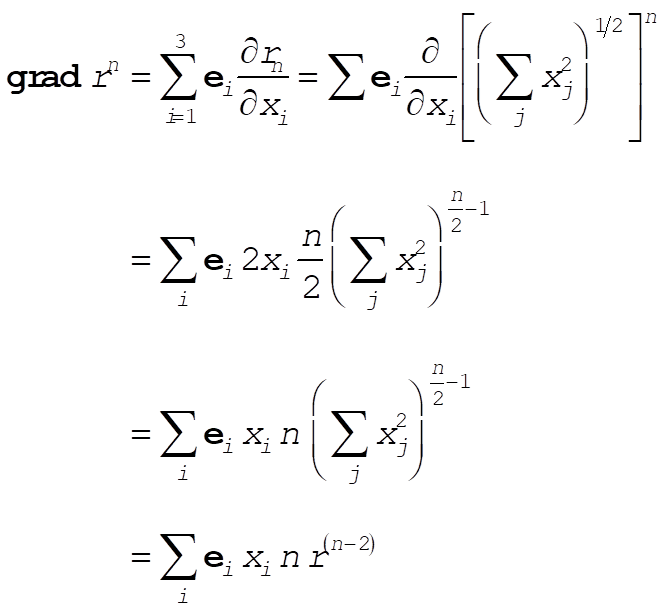 (1) (1)
Therefore,
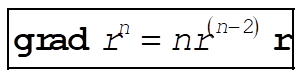 (2) (2)
b)
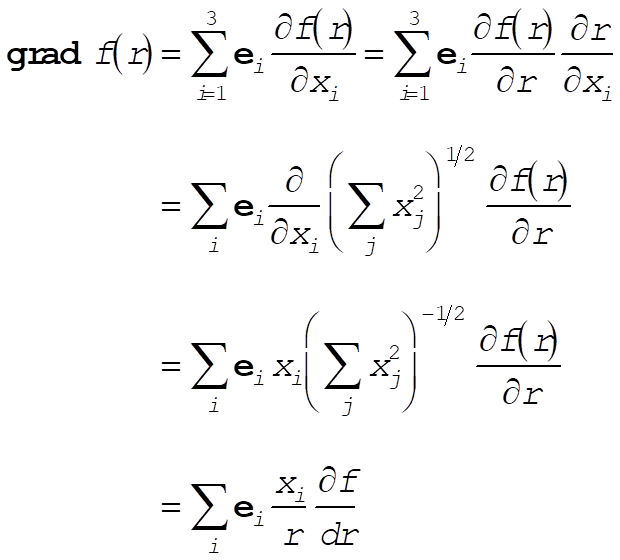 (3) (3)
Therefore,
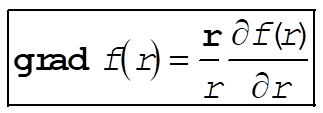 (4) (4)
c)
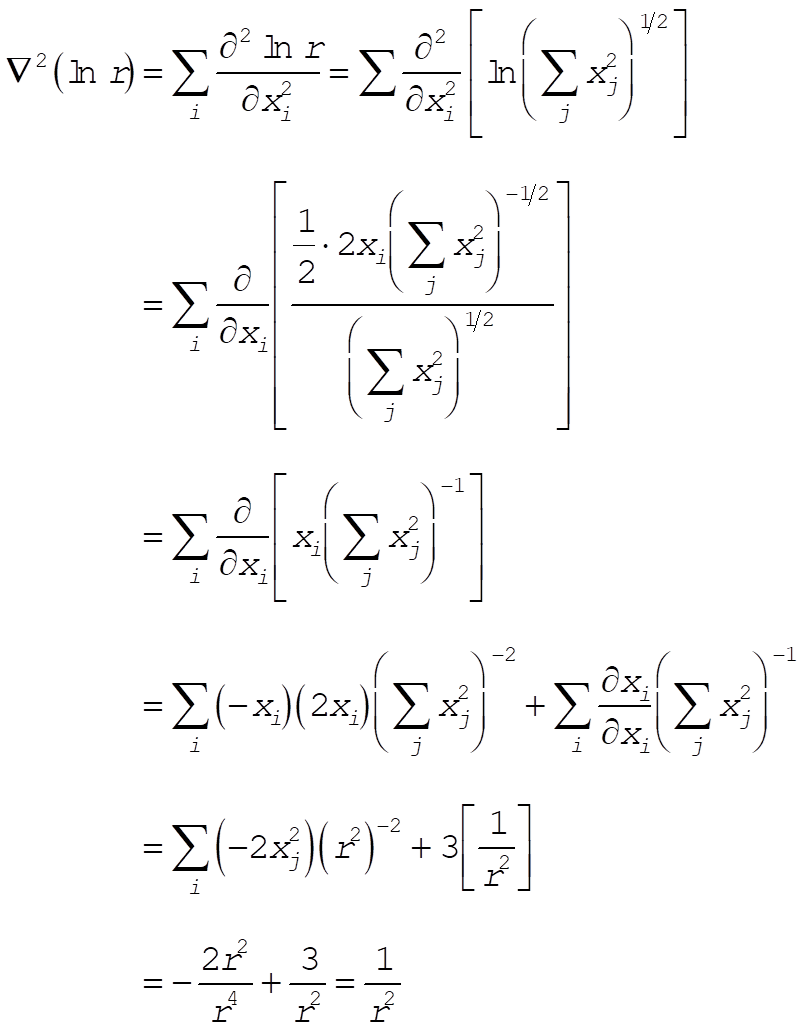 (5) (5)
or,
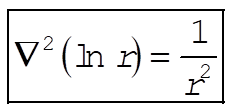 (6) (6)
1-33. Since
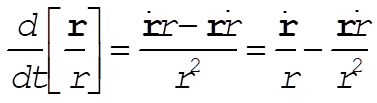 (1) (1)
we have
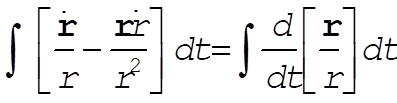 (2) (2)
from which
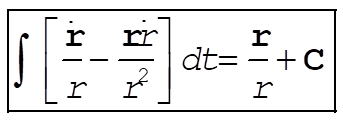 (3) (3)
where C is the integration constant (a vector).
1-37.
To do the integral directly, note that 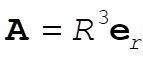 , on the surface, and that , on the surface, and that 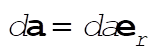 . .
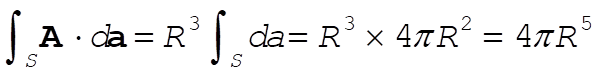 (1) (1)
To use the divergence theorem, we need to calculate 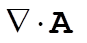 . This is best done in spherical coordinates, where . This is best done in spherical coordinates, where 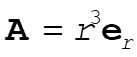 . Using Appendix F, we see that . Using Appendix F, we see that
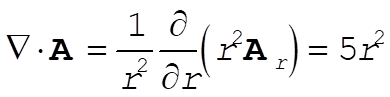 (2) (2)
Therefore,
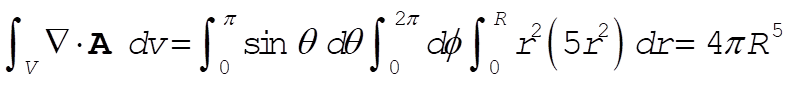 (3) (3)
Alternatively, one may simply set 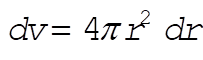 in this case. in this case.
Chapter 2
2-1. The basic equation is
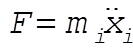 (1) (1)
a) 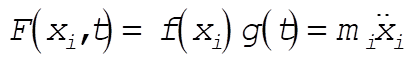 : Not integrable (2) : Not integrable (2)
b) 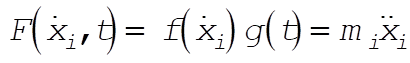
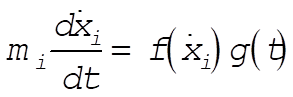
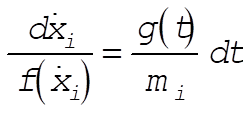 : Integrable (3) : Integrable (3)
c) 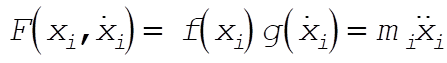 : Not integrable (4) : Not integrable (4)
2-5.
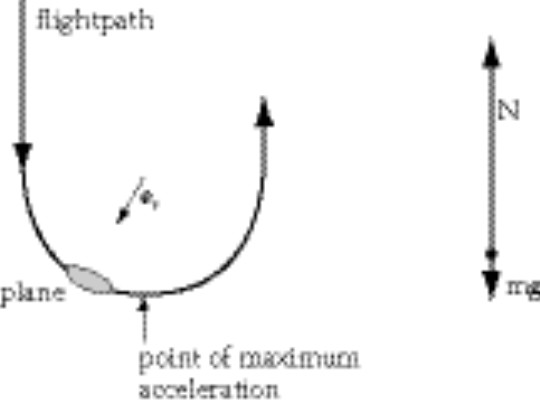
a) From the force diagram we have 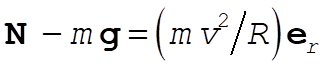 . The acceleration that the pilot feels is . The acceleration that the pilot feels is 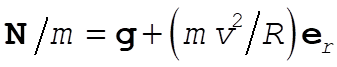 , which has a maximum magnitude at the bottom of the maneuver. , which has a maximum magnitude at the bottom of the maneuver.
b) If the acceleration felt by the pilot must be less than 9g, then we have
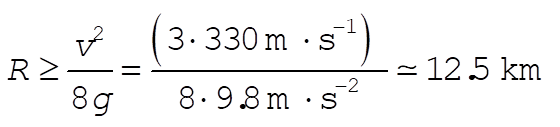 (1) (1)
A circle smaller than this will result in pilot blackout.
2-9.
a) Zero resisting force (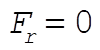 ): ):
The equation of motion for the vertical motion is:
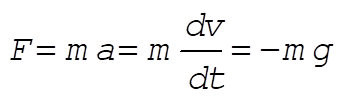 (1) (1)
Integration of (1) yields
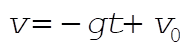 (2) (2)
where 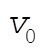 is the initial velocity of the projectile and t = 0 is the initial time. is the initial velocity of the projectile and t = 0 is the initial time.
The time 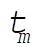 required for the projectile to reach its maximum height is obtained from (2). Since required for the projectile to reach its maximum height is obtained from (2). Since 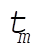 corresponds to the point of zero velocity, corresponds to the point of zero velocity,
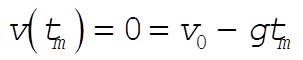 , (3) , (3)
we obtain
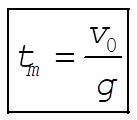 (4) (4)
b) Resisting force proportional to the velocity 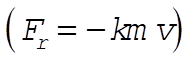 : :
The equation of motion for this case is:
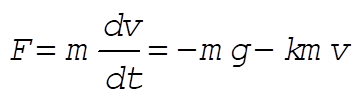 (5) (5)
where –kmv is a downward force for 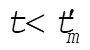 and is an upward force for and is an upward force for 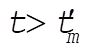 . Integrating, we obtain . Integrating, we obtain
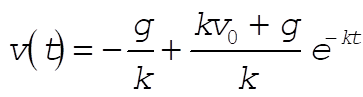 (6) (6)
For 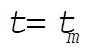 , v(t) = 0, then from (6), , v(t) = 0, then from (6),
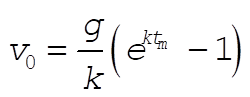 (7) (7)
which can be rewritten as
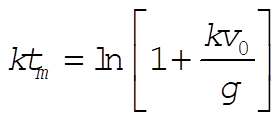 (8) (8)
Since, for small z (z = 1) the expansion
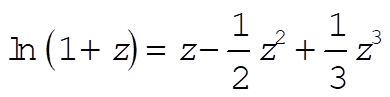 (9) (9)
is valid, (8) can be expressed approximately as
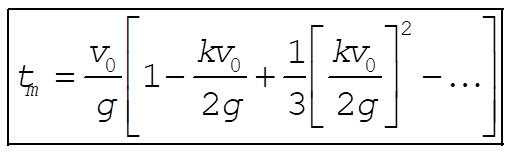 (10) (10)
which gives the correct result, as in (4) for the limit k ® 0.
2-13. The equation of motion of the particle is
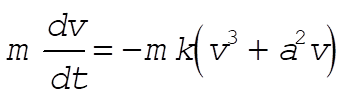 (1) (1)
Integrating,
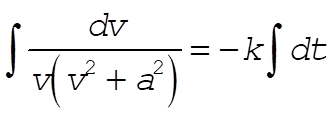 (2) (2)
and using Eq. (E.3), Appendix E, we find
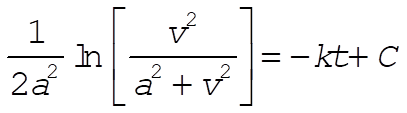 (3) (3)
Therefore, we have
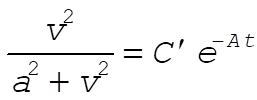 (4) (4)
where 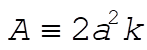 and where C¢ is a new constant. We can evaluate C¢ by using the initial condition, and where C¢ is a new constant. We can evaluate C¢ by using the initial condition, 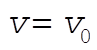 at t = 0: at t = 0:
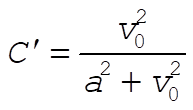 (5) (5)
Substituting (5) into (4) and rearranging, we have
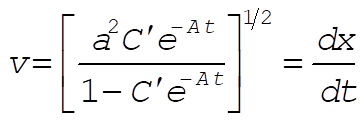 (6) (6)
Now, in order to integrate (6), we introduce 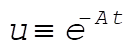 so that du = –Au dt. Then, so that du = –Au dt. Then,
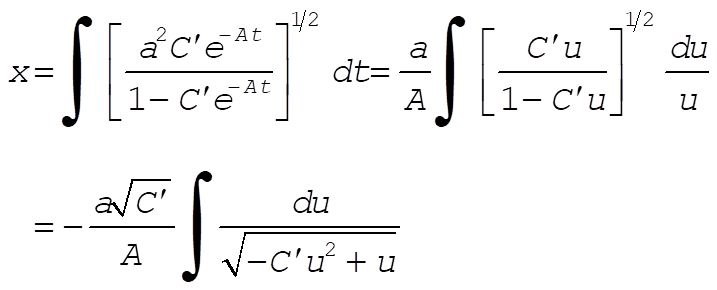 (7) (7)
Using Eq. (E.8c), Appendix E, we find
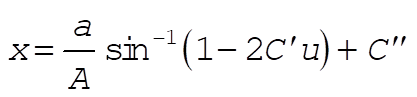 (8) (8)
Again, the constant C² can be evaluated by setting x = 0 at t = 0; i.e., x = 0 at u = 1:
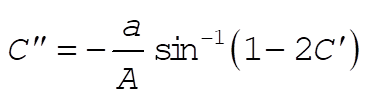 (9) (9)
Therefore, we have
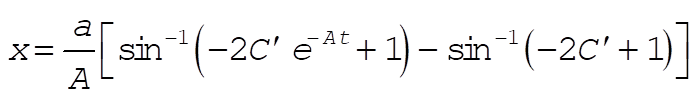
Using (4) and (5), we can write
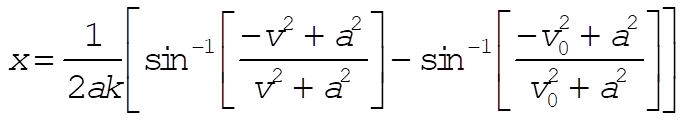 (10) (10)
From (6) we see that v ® 0 as t ® ¥. Therefore,
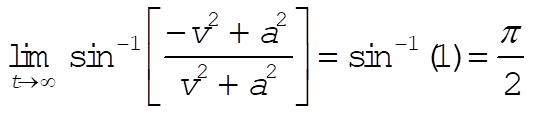 (11) (11)
Also, for very large initial velocities,
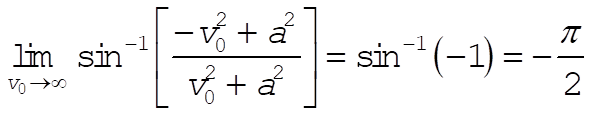 (12) (12)
Therefore, using (11) and (12) in (10), we have
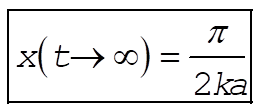 (13) (13)
and the particle can never move a distance greater than 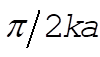 for any initial velocity. for any initial velocity.
2-17.
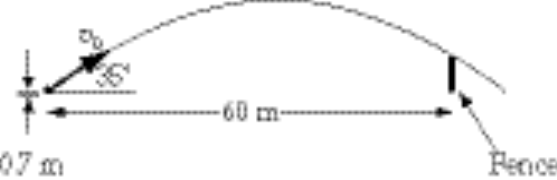
The setup for this problem is as follows:
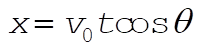 (1) (1)
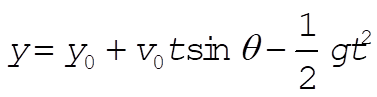 (2) (2)
where 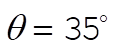 and and 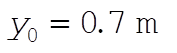 . The ball crosses the fence at a time . The ball crosses the fence at a time 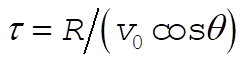 , where R = 60 m. It must be at least h = 2 m high, so we also need , where R = 60 m. It must be at least h = 2 m high, so we also need 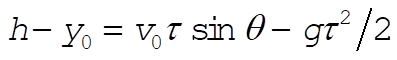 . Solving for . Solving for 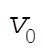 , we obtain , we obtain
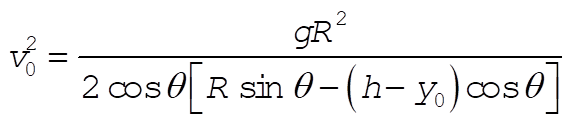 (3) (3)
which gives 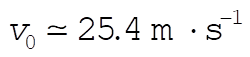 . .
At this point, you can go to the 3309 page,
the UH Space Physics Group
Web Site, or my personal Home Page.
Edgar A. Bering, III , <eabering@uh.edu>
|
 Homework 2
Homework 2