|
| |
Physics 3309 Homework 7
Chapter 5
5-13.
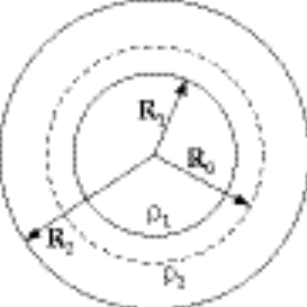
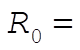 position of particle. For position of particle. For 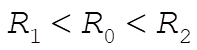 , we calculate the force by assuming that all mass for which , we calculate the force by assuming that all mass for which 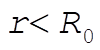 is at r = 0, and neglect mass for which is at r = 0, and neglect mass for which 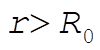 . The force is in the radially inward direction ( . The force is in the radially inward direction (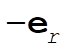 ). ).
The magnitude of the force is
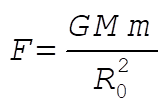
where M = mass for which 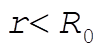
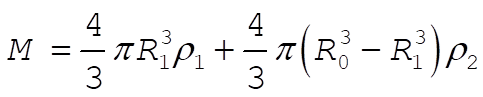
So 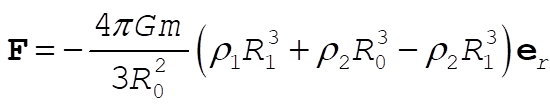
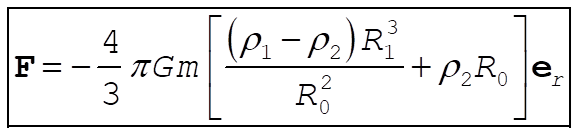
5-15. When the mass is at a distance r from the center of the Earth, the force is in the inward radial direction and has magnitude 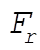 : :
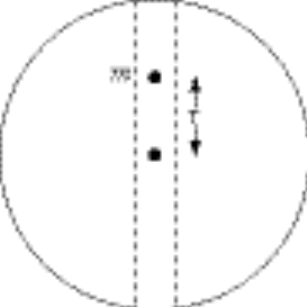
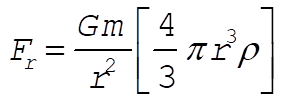 where r is the mass density of the Earth. The equation of motion is where r is the mass density of the Earth. The equation of motion is
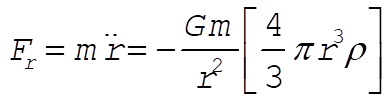
or
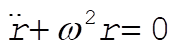 where where 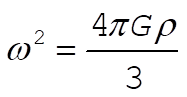
This is the equation for simple harmonic motion. The period is
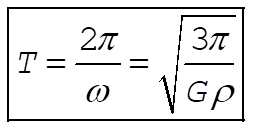
Substituting in values gives a period of about 84 minutes.
5-19.
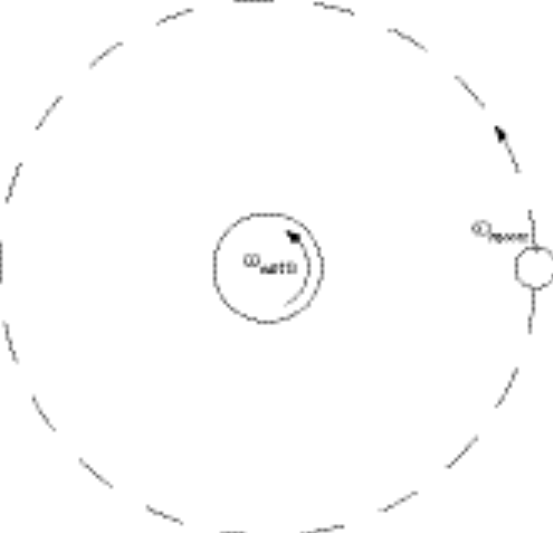
Because the moon’s orbit about the Earth is in the same sense as the Earth’s rotation, the difference of their frequencies will be half the observed frequency at which we see high tides. Thus
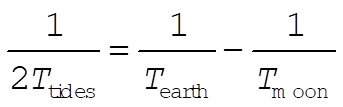 (1) (1)
which gives 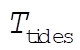 ; 12 hours, 27 minutes. ; 12 hours, 27 minutes.
Chapter 6
6-3. The element of distance in three-dimensional space is
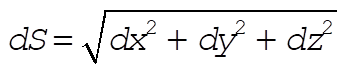 (1) (1)
Suppose x, y, z depends on the parameter t and that the end points are expressed by 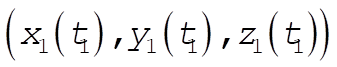 , , 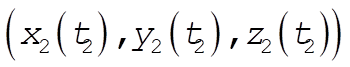 . Then the total distance is . Then the total distance is
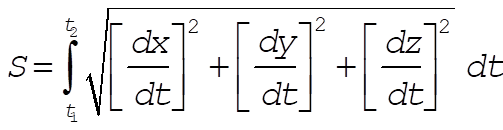 (2) (2)
The function f is identified as
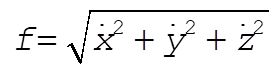 (3) (3)
Since 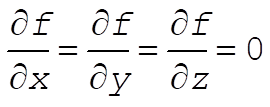 , the Euler equations become , the Euler equations become
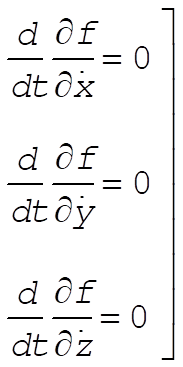 (4) (4)
from which we have
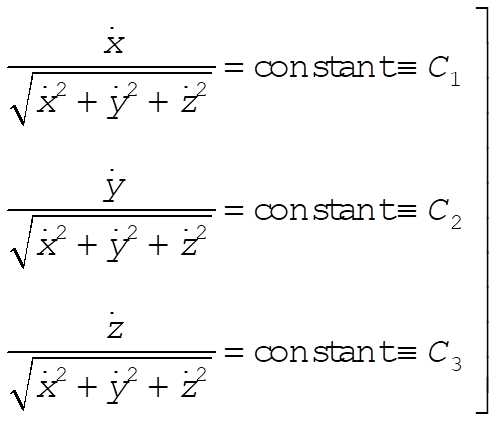 (5) (5)
From the combination of these equations, we have
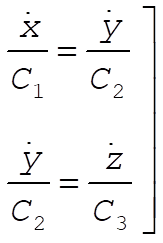 (6) (6)
If we integrate (6) from 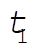 to the arbitrary t, we have to the arbitrary t, we have
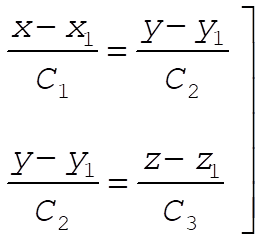 (7) (7)
On the other hand, the integration of (6) from 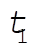 to to 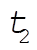 gives gives
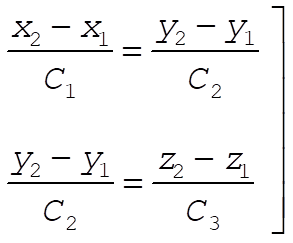 (8) (8)
from which we find the constants 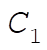 , , 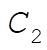 , and , and 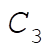 . Substituting these constants into (7), we find . Substituting these constants into (7), we find
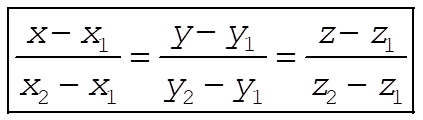 (9) (9)
This is the equation expressing a straight line in three-dimensional space passing through the two points 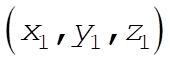 , , 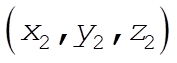 . .
6-7.

The time to travel the path shown is (cf. Example 6.2)
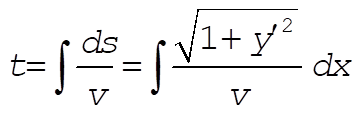 (1) (1)
Although we have v = v(y), we only have 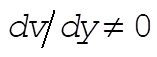 when y = 0. The Euler equation tells us when y = 0. The Euler equation tells us
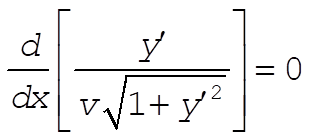 (2) (2)
Now use 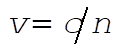 and y¢ = –tan q to obtain and y¢ = –tan q to obtain
n sin q = const. (3)
This proves the assertion. Alternatively, Fermat’s principle can be proven by the method introduced in the solution of Problem 6-8.
6-11.
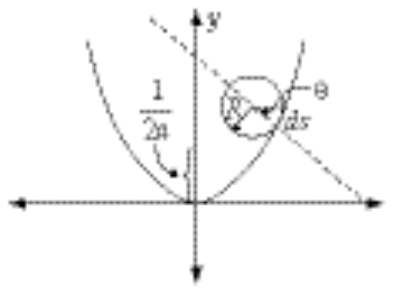
The constraint condition can be found from the relation ds = Rdq (see the diagram), where ds is the differential arc length of the path:
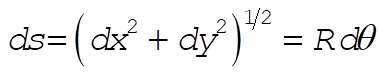 (1) (1)
which, using 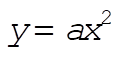 , yields , yields
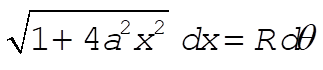 (2) (2)
If we want the equation of constraint in other than a differential form, (2) can be integrated to yield
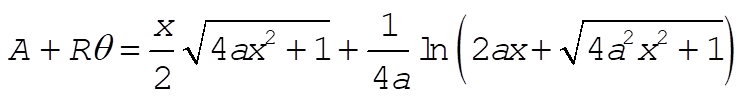 (3) (3)
where A is a constant obtained from the initial conditions. The radius of curvature of a parabola, 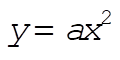 , is given at any point (x,y) by , is given at any point (x,y) by 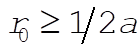 . The condition for the disk to roll with one and only one point of contact with the parabola is . The condition for the disk to roll with one and only one point of contact with the parabola is 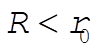 ; that is, ; that is,
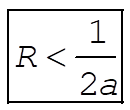
Chapter 7
7-3.
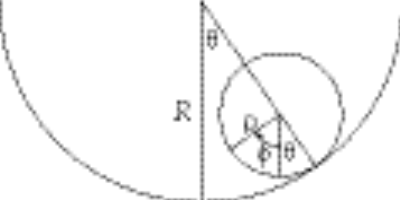
If we take angles q and f as our generalized coordinates, the kinetic energy and the potential energy of the system are
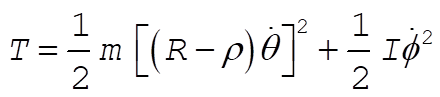 (1) (1)
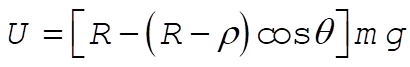 (2) (2)
where m is the mass of the sphere and where U = 0 at the lowest position of the sphere. I is the moment of inertia of sphere with respect to any diameter. Since 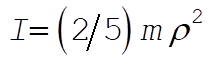 , the Lagrangian becomes , the Lagrangian becomes
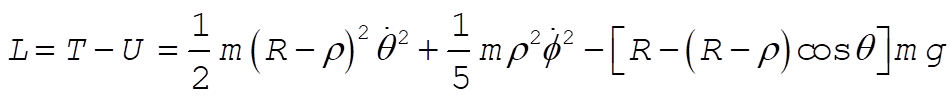 (3) (3)
When the sphere is at its lowest position, the points A and B coincide. The condition A0 = B0 gives the equation of constraint:
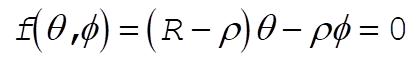 (4) (4)
Therefore, we have two Lagrange’s equations with one undetermined multiplier:
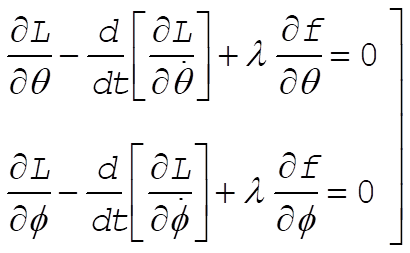 (5) (5)
After substituting (3) and 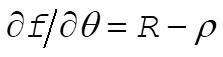 and and 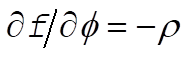 into (5), we find into (5), we find
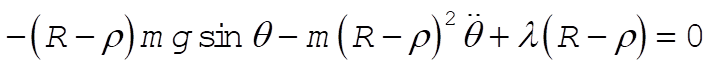 (6) (6)
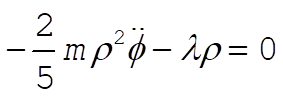 (7) (7)
From (7) we find l:
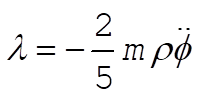 (8) (8)
or, if we use (4), we have
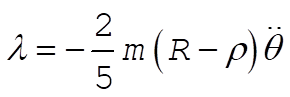 (9) (9)
Substituting (9) into (6), we find the equation of motion with respect to q :
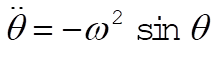 (10) (10)
where w is the frequency of small oscillations, defined by
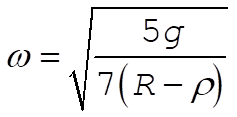 (11) (11)
7-7.
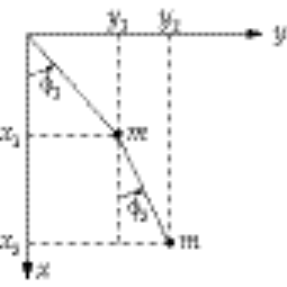
If we take 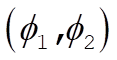 as our generalized coordinates, the x,y coordinates of the two masses are as our generalized coordinates, the x,y coordinates of the two masses are
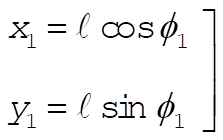 (1) (1)
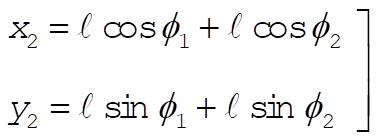 (2) (2)
Using (1) and (2), we find the kinetic energy of the system to be
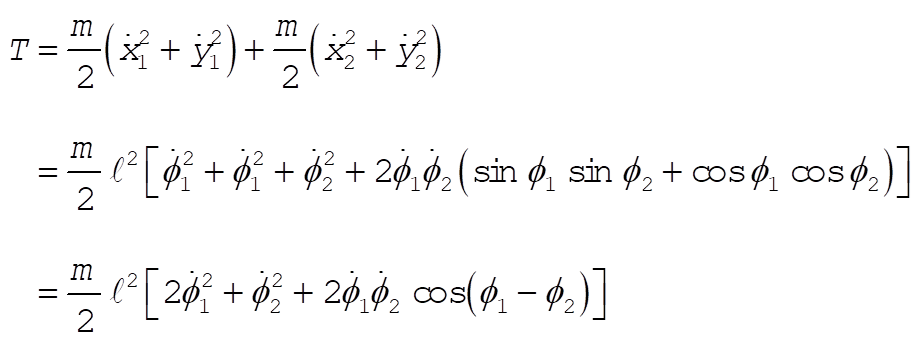 (3) (3)
The potential energy is
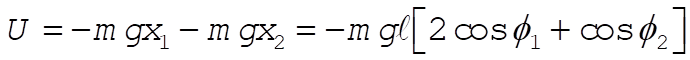 (4) (4)
Therefore, the Lagrangian is
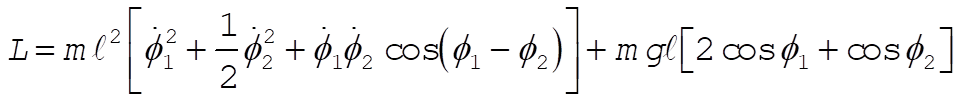 (5) (5)
from which
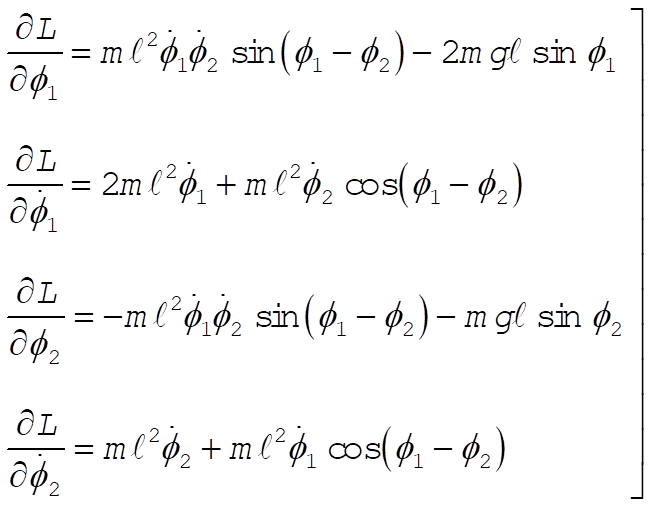 (6) (6)
The Lagrange equations for 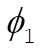 and and 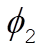 are are
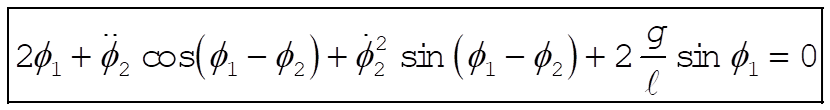 (7) (7)
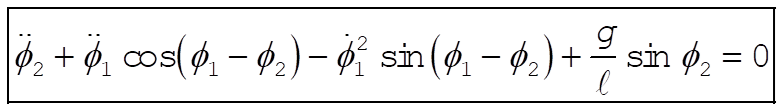 (8) (8)
At this point, you can go to the 3309 page,
the UH Space Physics Group
Web Site, or my personal Home Page.
Edgar A. Bering, III ,
Edgar A. Bering, III , <eabering@uh.edu>
|
 Homework 7
Homework 7