|
| |
Physics 3309 Homework 3
Chapter 2
2-21.
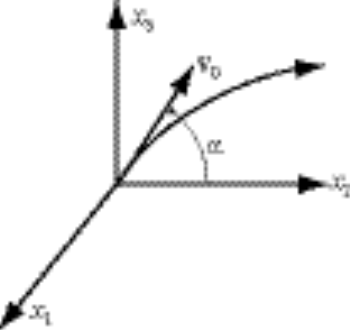
Assume a coordinate system in which the projectile moves in the 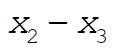 plane. Then, plane. Then,
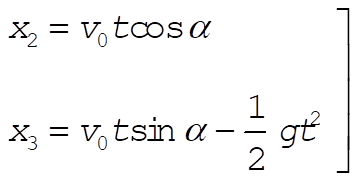 (1) (1)
or,
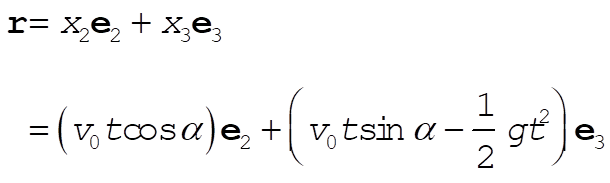 (2) (2)
The linear momentum of the projectile is
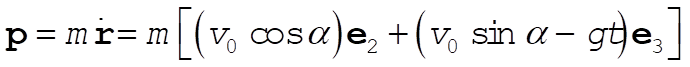 (3) (3)
and the angular momentum is
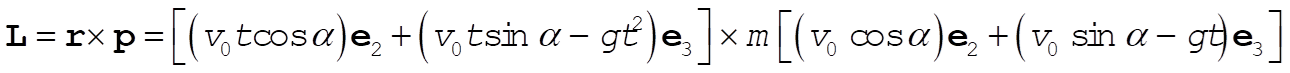 (4) (4)
Using the property of the unit vectors that 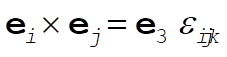 , we find , we find
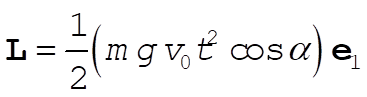 (5) (5)
This gives
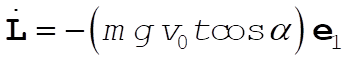 (6) (6)
Now, the force acting on the projectile is
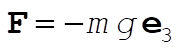 (7) (7)
so that the torque is
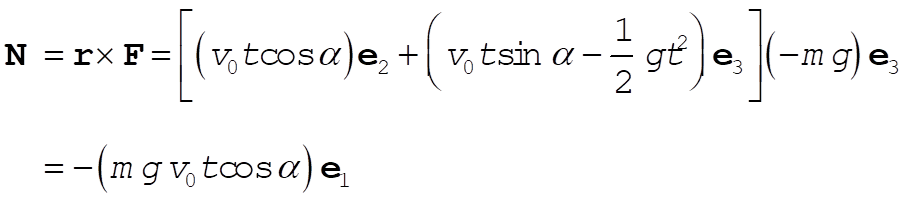
which is the same result as in (6).
2-22.
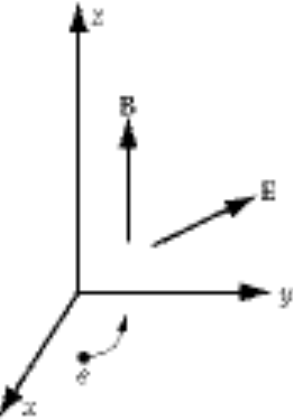
Our force equation is
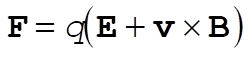 (1) (1)
a) Note that when E = 0, the force is always perpendicular to the velocity. This is a centripetal acceleration and may be analyzed by elementary means. In this case we have also 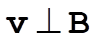 so that so that 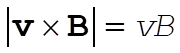 . .
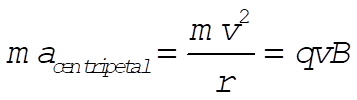 (2) (2)
Solving this for r
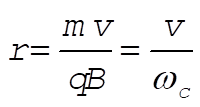 (3) (3)
with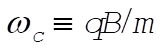 . .
b) Here we don’t make any assumptions about the relative orientations of v and B, i.e. the velocity may have a component in the z direction upon entering the field region. Let 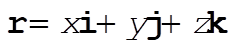 , with , with 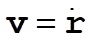 and and 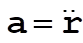 . Let us calculate first the v ´ B term. . Let us calculate first the v ´ B term.
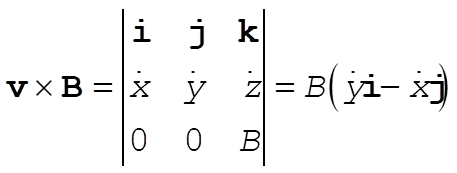 (4) (4)
The Lorentz equation (1) becomes
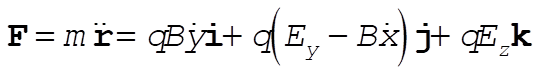 (5) (5)
Rewriting this as component equations:
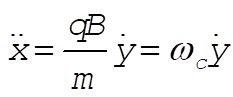 (6) (6)
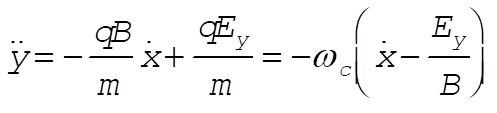 (7) (7)
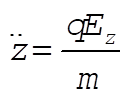 (8) (8)
The z-component equation of motion (8) is easily integrable, with the constants of integration given by the initial conditions in the problem statement.
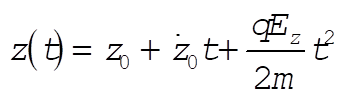 (9) (9)
c) We are asked to find expressions for 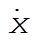 and and 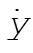 , which we will call , which we will call 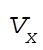 and and 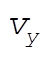 , respectively. Differentiate (6) once with respect to time, and substitute (7) for , respectively. Differentiate (6) once with respect to time, and substitute (7) for 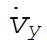
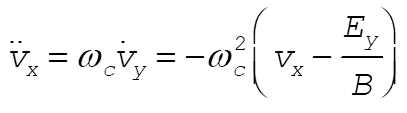 (10) (10)
or
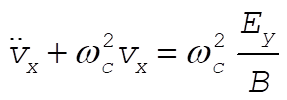 (11) (11)
This is an inhomogeneous differential equation that has both a homogeneous solution (the solution for the above equation with the right side set to zero) and a particular solution. The most general solution is the sum of both, which in this case is
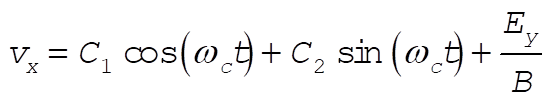 (12) (12)
where 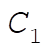 and and 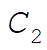 are constants of integration. This result may be substituted into (7) to get are constants of integration. This result may be substituted into (7) to get 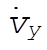
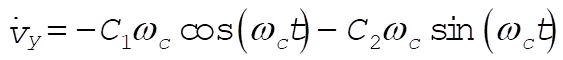 (13) (13)
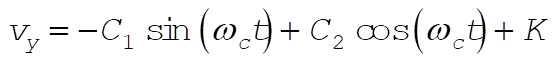 (14) (14)
where K is yet another constant of integration. It is found upon substitution into (6), however, that we must have K = 0. To compute the time averages, note that both sine and cosine have an average of zero over one of their periods 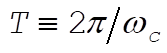 . .
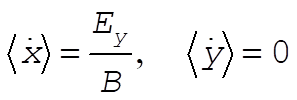 (15) (15)
d) We get the parametric equations by simply integrating the velocity equations.
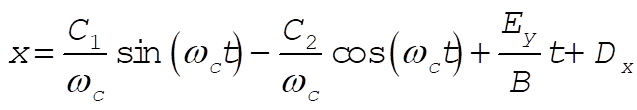 (16) (16)
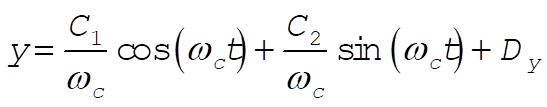 (17) (17)
where, indeed, 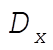 and and 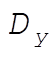 are constants of integration. We may now evaluate all the C’s and D’s using our initial conditions are constants of integration. We may now evaluate all the C’s and D’s using our initial conditions 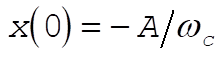 , , 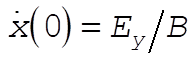 , , 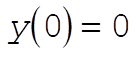 , , 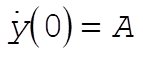 . This gives us . This gives us 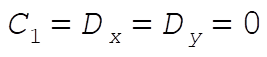 , , 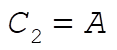 and gives the correct answer and gives the correct answer
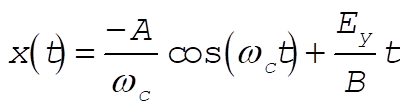 (18) (18)
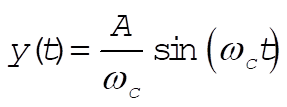 (19) (19)
These cases are shown in the figure as (i) 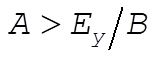 , (ii) , (ii) 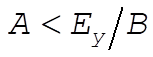 , and (iii) , and (iii) 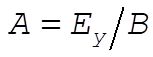 . .
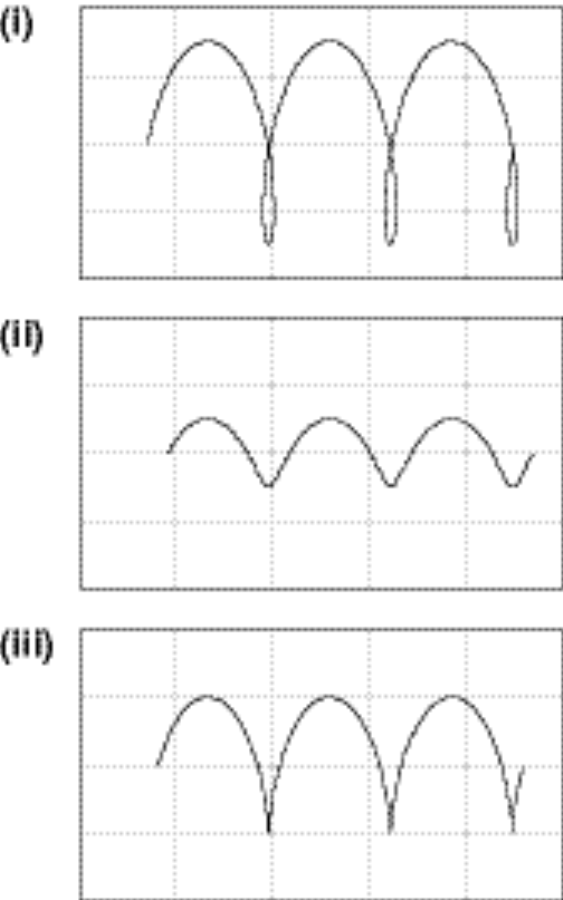
2-25.
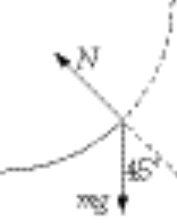
a) At A, the forces on the ball are:

The track counters the gravitational force and provides centripetal acceleration
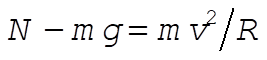
Get v by conservation of energy:
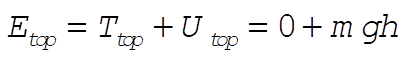
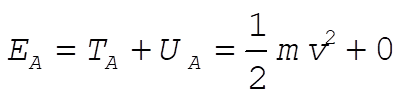
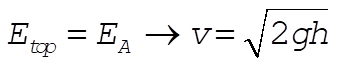
So
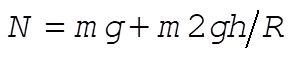
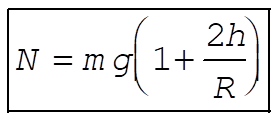
b) At B the forces are:
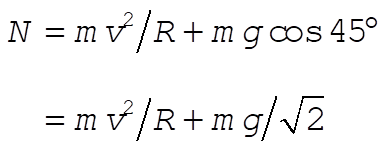 (1) (1)
Get v by conservation of energy. From a), 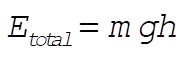 . .
At B, 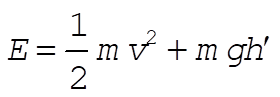
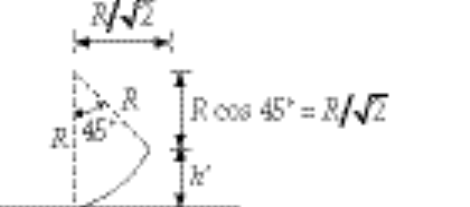
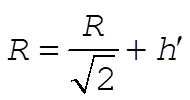 or or 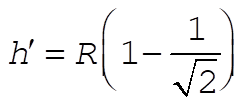
So  becomes: becomes:
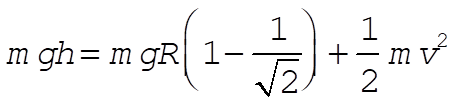
Solving for 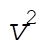
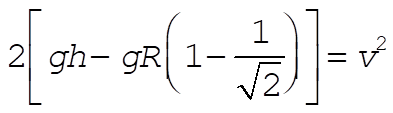
Substituting into (1):
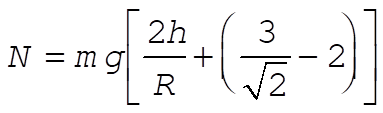
c) From b) 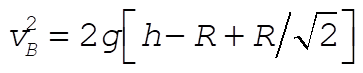
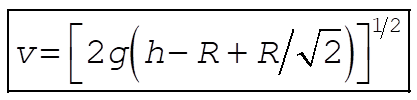
d) This is a projectile motion problem
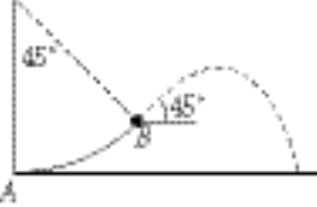
Put the origin at A.
The equations:
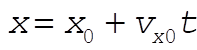
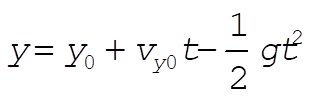
become
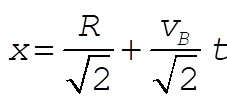 (2) (2)
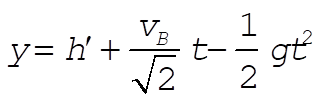 (3) (3)
Solve (3) for t when y = 0 (ball lands).
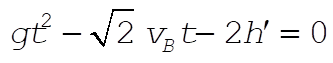
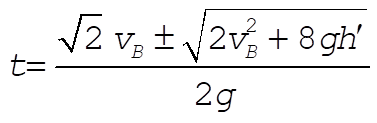
We discard the negative root since it gives a negative time. Substituting into (2):
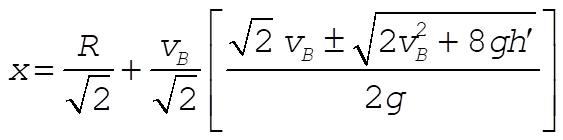
Using the previous expressions for 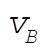 and h¢ yields and h¢ yields
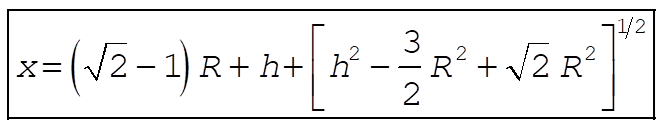
e) 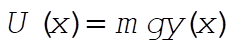 , with , with 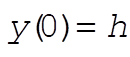 , so , so 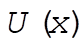 has the shape of the track. has the shape of the track.
2-29.
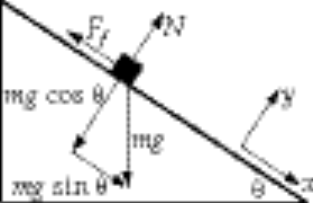
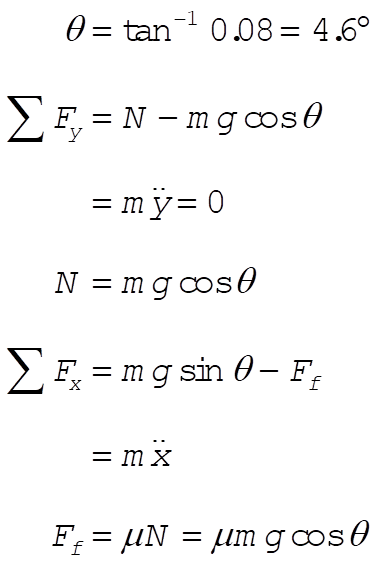
so
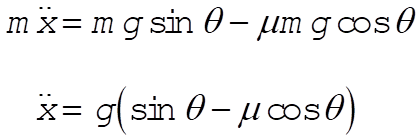
Integrate with respect to time
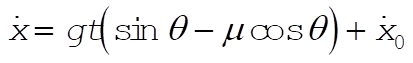 (1) (1)
Integrate again:
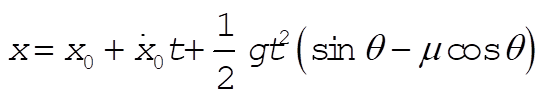 (2) (2)
Now we calculate the time required for the driver to stop for a given 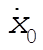 (initial speed) by solving Eq. (1) for t with (initial speed) by solving Eq. (1) for t with 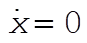 . .
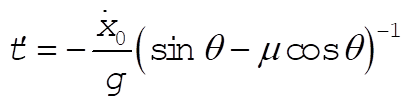
Substituting this time into Eq. (2) gives us the distance traveled before coming to a stop.
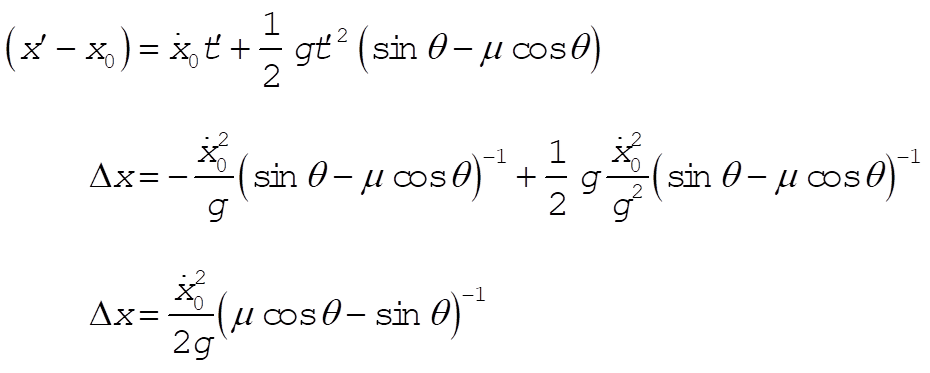
We have 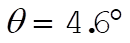 , , 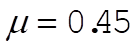 , , 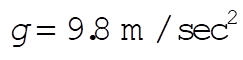 . .
For 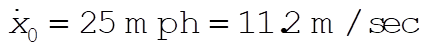 , , 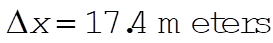 . .
If the driver had been going at 25 mph, he could only have skidded 17.4 meters.
Therefore, he was speeding
How fast was he going?
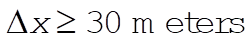 gives gives 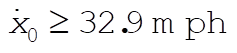 . .
2-31. For 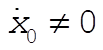 , example 2.10 proceeds as is until the equations following Eq. (2.78). Proceeding from there we have , example 2.10 proceeds as is until the equations following Eq. (2.78). Proceeding from there we have
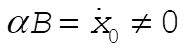
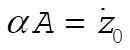
so
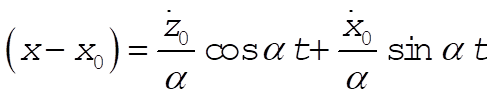
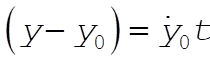
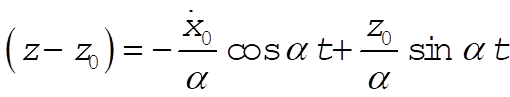
Note that
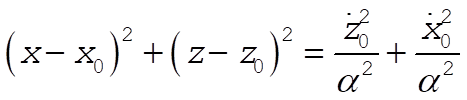
Thus the projection of the motion onto the x–z plane is a circle of radius 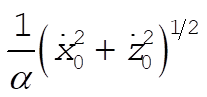 . .
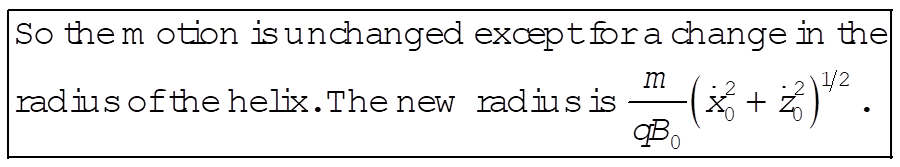
2-33. The differential equation to solve is
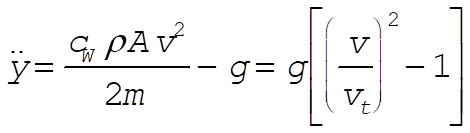 (1) (1)
where 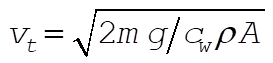 is the terminal velocity. The initial conditions are is the terminal velocity. The initial conditions are 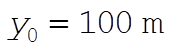 , and , and 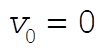 . The computer integrations for parts (a), (b), and (c) are shown in the figure. . The computer integrations for parts (a), (b), and (c) are shown in the figure.
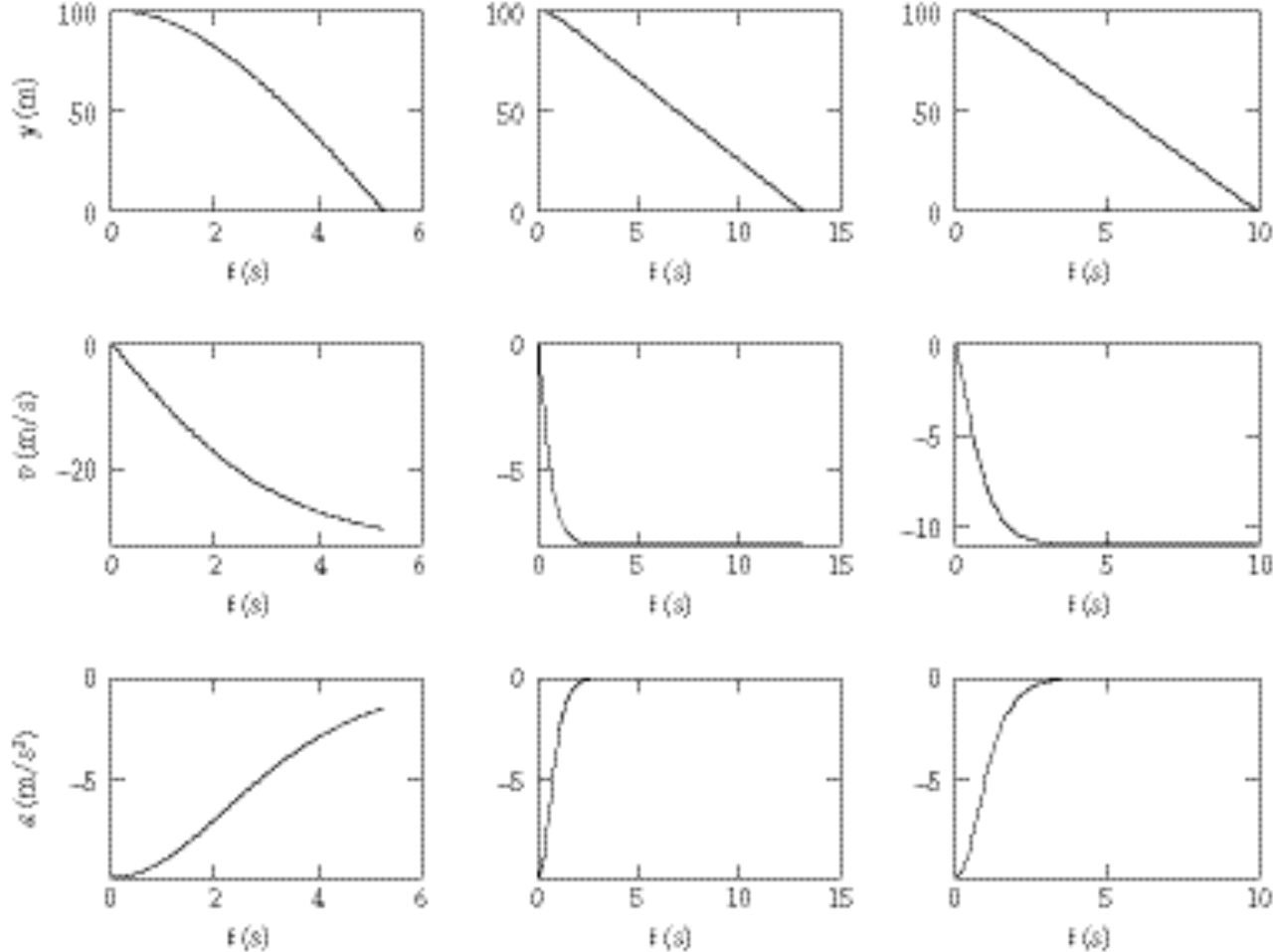
d) Taking 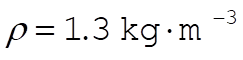 as the density of air, the terminal velocities are 32.2, 8.0, and 11.0 (all as the density of air, the terminal velocities are 32.2, 8.0, and 11.0 (all 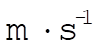 ) for the baseball, ping-pong ball, and raindrop, respectively. Both the ping-pong ball and the raindrop essentially reach their terminal velocities by the time they hit the ground. If we rewrite the mass as average density times volume, then we find that ) for the baseball, ping-pong ball, and raindrop, respectively. Both the ping-pong ball and the raindrop essentially reach their terminal velocities by the time they hit the ground. If we rewrite the mass as average density times volume, then we find that 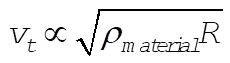 . The differences in terminal velocities of the three objects can be explained in terms of their densities and sizes. . The differences in terminal velocities of the three objects can be explained in terms of their densities and sizes.
e) Our differential equation shows that the effect of air resistance is an acceleration that is inversely proportional to the square of the terminal velocity. Since the baseball has a higher terminal velocity than the ping-pong ball, the magnitude of its deceleration is smaller for a given speed. If a person throws the two objects with the same initial velocity, the baseball goes farther because it has less drag.
f) We have shown in part (d) that the terminal velocity of a raindrop of radius 0.004 m will be larger than for one with radius 0.002 m (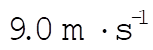 ) by a factor of ) by a factor of 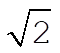 . .
2-37. 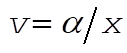 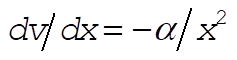
Since 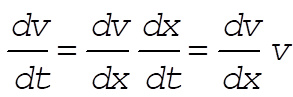 then then
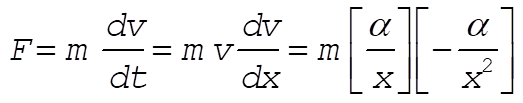
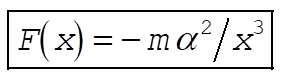
2-39.
a) 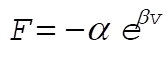
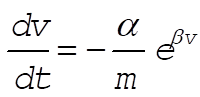
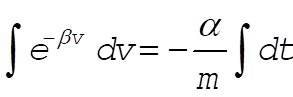
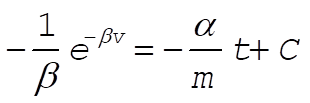
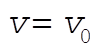 at t = 0, so at t = 0, so
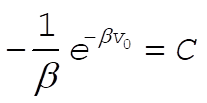
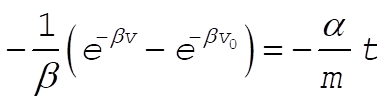
Solving for v gives
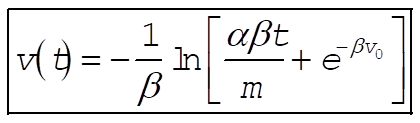
b) Solve for t when v = 0
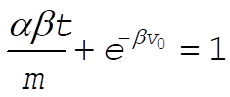
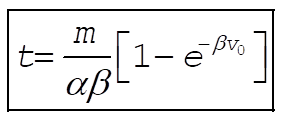
c) From a) we have
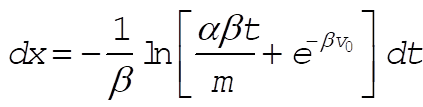
Using 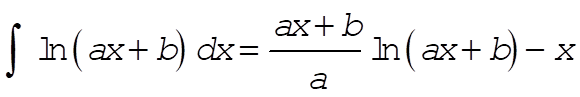 we obtain we obtain
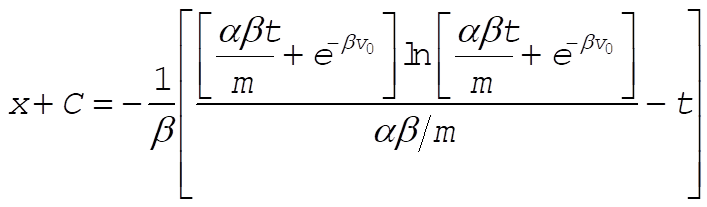
Evaluating C using x = 0 at t = 0 gives
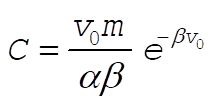
So
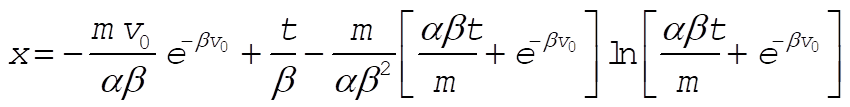
Substituting the time required to stop from b) gives the distance required to stop
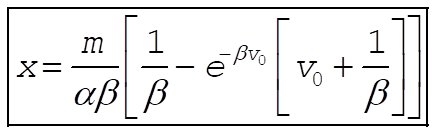
At this point, you can go to the 3309 page,
the UH Space Physics Group
Web Site, or my personal Home Page.
Edgar A. Bering, III ,<eabering@uh.edu>
|
 Homework 3
Homework 3